Методы оптимизации в технико-экономических задачах

2.

Задача линейного планирования производства

Теоретическая часть

Задачи линейного программирования находят широкое распространение в различных областях:

· Энергетике - рациональная организация электрификации районов с помощью различных видов электростанций;

· Химии - составление сложных смесей с заданным составом компонентов;

· Сельском хозяйстве - рациональное распределение посевных площадей под различные культуры;

· Металлургии- расчёт шихты для получения специальных легированных сталей;

Несмотря на такое многообразие, существуют способы перехода от всех частных задач к основной задаче линейного программирования. Она формулируется следующим образом.

Для переменных x1, x2, … , xn найти такие неотрицательные значения

xj≥0, j=1 n

которые обращали бы в максимум целевую функцию

F=c0+→ max

и удовлетворяли системе равенств

i=1 m

Симплексный метод или метод последовательного улучшения плана основан на идее перехода от одного базисного решения в вершине многоугольника допустимых решений к другому базисному решению, более близкому к оптимальному. Предполагается, что ранг системы равен числу уравнений m и меньше числа переменных n.

Если неизвестных переменных n, а ограничений m, то можно m неизвестных выразить через остальные (n-m) переменных, которые играют роль произвольных постоянных и называются свободными. Те m неизвестных переменных, которые выражаются через свободные, называются базисными.

Решение называется базисом, если в нем m базисных неизвестных выражены через (n-m) свободных неизвестных, и при равенстве свободных неизвестных нулю, что предполагается в базисном решении, базисные неизвестные неотрицательны.

Пронумеруем переменные таким образом, чтобы вначале шли свободные переменные (x1, … , xk), а далее базисные переменные (xk+1 , … , xn)

, x2, … , xk, xk+1, xk+2, … , xk+i, … , xn

Выразим базисные переменные и целевую функцию через свободные переменные:

+i=bi - i=1 m=c0+→ max

При решении задач линейного программирования принято находить минимум целевой функции, то есть f(x) → min, где f(x)=-F(x)

Существует несколько методов решения задач линейного программирования:

1. графоаналитический метод;

2. симплекс-метод;

В графоаналитическом методе следует учитывать что переменных должно быть не более двух. Здесь сначала на основе неравенств строится область допустимых значений. Любое неравенство двух переменных делит область на два подмножества: в одном они выполняются, в другом - нет. Подмножества представляют собой полуплоскости, разделяемые прямой, которая получается, если в ограничении заменить знак неравенства на знак равенства.

Затем находится градиент, если функцию необходимо минимизировать, и антиградиент функции, если максимизировать:

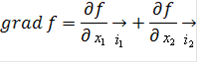
Значение функции будет уменьшаться при движении по направлению антиградиента, и увеличиваться по направлению градиента.

Далее следует уловить тот момент, в котором эта линия имеет последнюю общую точку с ОДР.

Симплекс-методом получивший также в литературе название метода последовательного улучшения плана, разработанный в 1947г. американским математиком Джорджем Данцигом. Он даёт аналитическое решение задачи для любого количества переменных и удобен в использовании.

Для решения задачи линейного программирования симплекс-методом все ограничения должны иметь вид равенств.

Первый этап решения задач симплекс-методом сводится к приведению задачи к канонической форме.

Второй этап представляет собой выбор начального базиса. Обычно в качестве базисных переменных выбирают те, которые изначально заданы в неравенствах.

Третий этап заключается в выражении целевой функции через свободные неизвестные. Для этого необходимо выразить все базисные переменные через свободные, а затем, подставить их в выражение для целевой функции.